《人工智能的数学基础》《Mathematical Basis of Artificial Intelligence》教学大纲-计算机科学与工程学院（人工智能学院）

《人工智能的数学基础》《Mathematical Basis of Artificial Intelligence》教学大纲

制定时间：2025 年 2 月

一、课程基本信息

（一）适用专业

智能科学与技术

（二）课程代码

（三）学分/课内学时

3学分/48学时

（四）课程类别

专业教育

（五）课程性质

必修/理论课

（六）先修课程

《线性代数》、《高等数学》、《概率论与数理统计》等

（七）后续课程

《深度学习》、《强化学习》、《毕业设计》等

二、课程教学目标

（一）课程定位

《人工智能的数学基础》是智能科学与技术等专业的专业必修课，是人工智能领域的核心先导课程，旨在为学习者构建支撑AI理论与技术的数学知识体系。课程定位于连接基础数学与AI应用的桥梁，面向具备高等数学、线性代数基础的学生，聚焦于机器学习、深度学习等AI分支中不可或缺的数学工具。内容涵盖概率统计（贝叶斯推理、分布建模）、优化理论（梯度下降、凸优化）、线性代数（矩阵分解、张量运算）、信息论（熵与编码）以及图论（网络结构与知识图谱），通过理论推导与实例解析（如反向传播的链式法则、主成分分析的矩阵分解），揭示数学原理在模型设计、算法优化中的底层逻辑。课程强调数学形式化思维与工程问题建模能力的双重培养，为后续《机器学习》《计算机视觉》等应用型课程奠定严格的数理基础，助力学生从“调参实践”向“原理创新”进阶。

（二）总体目标

《人工智能的数学基础》课程旨在构建支撑人工智能核心技术的关键数学能力体系，培养学习者从数学本质理解算法原理、优化模型及解决复杂问题的思维模式。通过系统学习概率论与统计推断（如贝叶斯网络、马尔可夫链）、线性代数与张量运算（如特征值分解、矩阵求导）、凸优化理论（如梯度下降、拉格朗日对偶性）以及信息论（如熵、KL散度）等核心内容，学生能够掌握AI模型设计的数学逻辑（如神经网络反向传播的微分链式法则、注意力机制的权重分配原理），并具备将数学公式转化为代码实现的能力。课程强调从数学严谨性出发，提升对算法泛化性、可解释性的分析能力，为机器学习、深度学习等高阶课程奠定理论根基，同时助力解决工业场景中的模型调优、数据分布建模等实际问题，推动从“应用调用”到“理论突破”的创新能力进阶。

（三）教学目标

本课程旨在系统构建学生支撑人工智能技术的核心数学能力，聚焦概率统计、线性代数、优化理论与信息论等领域的核心工具，培养从数学本质理解算法原理的思维模式。通过理论推导与实例解析（如反向传播的微分链式法则、主成分分析的矩阵分解），学生能够掌握数学形式化语言描述模型的能力，理解算法设计的数学逻辑（如梯度下降的收敛性、贝叶斯推断的统计基础）。同时，课程强调数学理论与工程实践的融合，训练学生将复杂问题建模为数学优化问题（如分类任务转化为概率分布拟合问题），并利用工具（如NumPy、PyTorch）实现数学公式的代码化验证，为深度学习、自然语言处理等应用课程奠定严格的数理基础，助力从“调参实践”到“理论创新”的思维跃迁。

1.具体目标

目标1：数学工具的形式化表达与推导能力：掌握概率论（贝叶斯定理、马尔可夫链）、线性代数（矩阵分解、张量运算）等核心数学工具，能够严格推导AI算法的数学原理（如神经网络的梯度更新公式、注意力机制的权重分配原理）。

目标2：数学建模与算法优化能力：能够将实际问题转化为数学优化问题，掌握凸优化、信息论（熵、KL散度）等工具设计高效算法并验证理论性能。通过案例驱动，强化从建模、求解到工程落地的全链路能力。

2.课程目标与毕业要求的对应关系

毕业要求

毕业要求指标点

课程

目标

教学

单元

评价

方式

1. 掌握专业必需的数学、自然科学、工程基础和专业知识，能够用于解决智能系统开发中的复杂工程问题。

1.3:智能科学与技术专业的基本理论、基本知识，掌握扎实的工程基础知识。

目标1

1-7

平时作业，实验，

试卷考核

4. 能够基于科学原理，采用适当的工程方法对智能系统的复杂工程问题进行研究，包括系统方案设计、分析与解释数据、并通过信息综合得到合理有效的结论。

4.2: 能够基于智能科学与技术专业相关理论和对象特征，选择研究开发路线和设计可行的系统方案。

目标2

4-6,8

平时作业，实验，

试卷考核

三、教学内容与方法

（一）教学内容及要求

序号	教学单元	教学内容	学习产出要求	推荐学时	推荐教学方式	课程目标	备注
1	代数学和分析学的基本概念	代数学：向量，范数，矩阵，行列式的定义和性质。分析学：极限、连续性的定义和性质。	1掌握向量，范数，矩阵，行列式的基本运算规则。 2能基于连续性分析，证明简单优化问题（如线性回归）解的存在性，并解释激活函数连续性与模型稳定性的关联。	4	讲授	1
2	微积分的基础概念	单变量微积分：导数、微分、泰勒展开，梯度与极值判定。多变量微积分：偏导数、方向导数、梯度向量与Hessian矩阵。	1能准确定义导数、微分与泰勒展开的数学意义，解释其在函数局部线性逼近中的作用。 2能计算多项式、指数、对数等基本函数的导数与微分，推导简单复合函数的链式法则。	4	讲授	1
3	矩阵与线性变换	矩阵运算：加法、乘法、转置，张量的多维表示。线性变换：基变换、特征值/向量，仿射变换的几何意义。	1掌握矩阵的基本操作，比如加法、乘法和转置。 2能计算矩阵的特征值和特征向量，理解矩阵乘法与线性变换的关系。 3理解基变换如何改变坐标系。 4基础工具实验：熟悉Python/Matlab基础、NumPy/Pandas数学库操作（矩阵运算、概率分布可视化）。	4	讲授、实验	1
4	矩阵分解	核心分解：SVD（奇异值分解）、QR分解、LU分解的原理与数值稳定性。应用场景：SVD用于推荐系统协同过滤，QR分解求解线性方程组。	1理解SVD、QR、LU分解的数学原理与数值稳定性，能编程实现图像/数据压缩； 2解释协同过滤与线性方程组求解的分解应用，分析不同场景下分解方法的选择依据。	8	讲授、实验	1，2
5	最优化理论与算法	凸优化基础：凸集、凸函数、拉格朗日对偶性，KKT条件。算法设计：梯度下降、牛顿法、Adam优化器的收敛性证明。	1掌握凸优化问题的数学建模与对偶转化，能推导KKT条件求解带约束优化。 2对比梯度下降、牛顿法与Adam的收敛性差异，编程实现并分析参数对算法性能的影响。 3理解并掌握神经网络的权重更新策略。	8	讲授、实验	1，2
6	概率模型	概率基础：随机变量及分布，随机变量的数字特征。极限理论：大数定律，中心极限定理。参数估计：最大似然估计，贝叶斯估计	1掌握随机变量分布特性及期望方差计算。 2应用大数定律分析蒙特卡洛模拟收敛性。 3能推导最大似然估计并实现贝叶斯参数推断，解释其在模型训练与不确定性量化中的作用。	8	讲授、实验	1，2
7	信息论的基础概念	核心度量：熵、交叉熵、KL散度、互信息的定义与性质。	1掌握信息熵、交叉熵与KL散度的计算，能应用互信息进行特征选择。 2能计算图像数据集各通道的信息熵，设计基于互信息的特征选择策略提升分类模型准确率。	4	讲授、实验	1
8	信息论在机器学习中的应用	应用场景：KL散度在机器学习中的应用、模型压缩（熵编码）	1能解释KL散度在变分自编码器（VAE）正则化中的作用，并通过调整KL权重参数分析生成图像质量的平衡关系。	8	讲授、实验	2

（二）教学方法

1.课堂讲授

课堂讲授的目的是使得学生能从数学本质理解算法原理、优化模型及解决复杂问题的思维模式。本课程共设置8个课堂讲授单元，具体特点如下：

（1）采用启发式教学，激发学生主动学习的兴趣，培养学生独立思考、分析问题和解决问题的能力，引导学生主动通过实践和自学获得自己想学到的知识。

（2）在教学内容上，采用数学-AI双视角教学，避免孤立讲授数学，始终以AI问题为锚点。通过“猜想-验证-改进”模式引导学生探索数学本质。从基础数学工具（微积分、矩阵分解）到高阶模型（VAE、强化学习），建立“公式→代码→系统”的完整链路。

（3）在教学过程中采用电子教案、CAI课件、多媒体教学与传统板书、教具教学相结合，提高课堂教学信息量，增强教学的直观性。

（4）理论教学与工程实践相结合，引导学生应用数学、自然科学和工程科学的基本原理，为具备解决相关工程问题思维方法和实践能力奠定基础。

（6）课内讨论和课外答疑相结合，每个月至少进行一次答疑。

2.实验教学

实验教学的目的是培养学生掌握AI模型设计的数学逻辑，并具备将数学公式转化为代码实现的能力，建立“公式→代码→系统”的完整链路。本课程共设置6个实验单元，包括

基础工具实验：Python/Matlab基础、NumPy/Pandas数学库操作（矩阵运算、概率分布可视化）；（2课时）
核心算法验证：线性回归、梯度下降实现、贝叶斯分类器推导、SVM优化问题求解；（6课时）
综合应用项目：基于概率图模型的简单推理、神经网络反向传播手写推导与代码实现。（4课时）

具体特点如下：

（1）数学公式与代码的双向映射：实验设计紧扣数学理论，要求学生将抽象公式转化为可执行代码，同时通过实验结果反向验证数学原理。

（2）真实场景与数据集驱动：使用Kaggle或公开数据集（如MNIST、CIFAR-10），在图像分类任务中应用PCA降维，分析数学工具对模型效率的提升。

（3）可视化与交互式分析：利用Matplotlib或Plotly绘制损失函数曲面、梯度下降轨迹，直观展示优化过程（如对比SGD与Adam的收敛路径）。

（4）独立性和完整性：实验由学生独立完成并撰写相应的实验报告，力图使得每个同学都能建立“公式→代码→系统”的完整链路。

（5）严格的可复现性要求：要求实验代码模块化，附带详细数学注释。报告需包含数学推导、结果可视化与工程反思。

四、考核及成绩评定

（一）考核内容及成绩构成

课程考核以考核学生能力培养目标的达成为主要目的，以检查学生对各知识点的掌握程度和应用能力为重要内容，包括平时考核和期末考核两个部分。平时考核采用实验报告方式评定学生成绩；期末考核采用期末考试评定学生成绩。各课程目标的考核内容、成绩评定方式、目标分值建议如下：

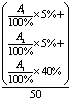
课程目标	考核内容	成绩评定方式	成绩占总评分比例	目标成绩占当次考核比例	学生当次考核平均得分	目标达成情况计算公式
目标1：数学工具的形式化表达与推导能力：掌握概率论（贝叶斯定理、马尔可夫链）、线性代数（矩阵分解、张量运算）等核心数学工具，能够严格推导AI算法的数学原理（如神经网络的梯度更新公式、注意力机制的权重分配原理）。	1. 向量，范数，矩阵，行列式的基本运算规则 2. 计算矩阵的特征值和特征向量 3. 矩阵分解步骤复现 4. 梯度下降、牛顿法、Adam优化器的收敛性证明。 5. 能推导最大似然估计并实现贝叶斯参数推断	实验1	5%	100%	A₁
		实验2	5%	100%	A₂
		期末考试	40%	70%	A₃
目标2：数学建模与算法优化能力：能够将实际问题转化为数学优化问题，掌握凸优化、信息论（熵、KL散度）等工具设计高效算法并验证理论性能。通过案例驱动，强化从建模、求解到工程落地的全链路能力。	1. 对比梯度下降、牛顿法与Adam的收敛性差异。 2. 解释线性方程组求解的分解应用，分析不同场景下分解方法的选择依据。 3. 计算图像数据集各通道的信息熵，设计基于互信息的特征选择策略提升分类模型准确率。	实验3	10%	100%	B₁
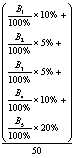
		实验4	5%	100%	B₂
		实验5	5%	100%	B₃
		实验6	10%	100%	B₄
		期末考试	20%	30%	B₅
总评成绩（100%）=平时实验（40%）+期末考试（60%）			100%	——	——

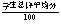
（二）平时考核成绩评定

1.平时实验

本课程共设计实验6次，其中6次需要提交实验报告，支撑目标1和目标2，共占总评分40%，其中目标1占10%，目标2占30%。对应目标的评分标准如下：

对应目标		目标1：数学工具的形式化表达与推导能力：掌握概率论（贝叶斯定理、马尔可夫链）、线性代数（矩阵分解、张量运算）等核心数学工具，能够严格推导AI算法的数学原理（如神经网络的梯度更新公式、注意力机制的权重分配原理）。目标2：数学建模与算法优化能力：能够将实际问题转化为数学优化问题，掌握凸优化、信息论（熵、KL散度）等工具设计高效算法并验证理论性能。通过案例驱动，强化从建模、求解到工程落地的全链路能力。
成绩比例		40%
考查点		实验内容完成情况	实验报告情况
评分标准	100% 至90%	根据实验要求实现主要功能，同时完成附加任务要求。实验态度认真，充分理解实验要求，解决问题能力强，沟通协作能力很好。	实验报告完整，内容丰富、图文并茂，文字足够且正确，对实验方案有自己独到的思路与见解。
	89.9% 至80%	根据实验要求实现主要功能。实验态度认真，理解实验要求，解决问题能力较强，沟通协作能力较强。	实验报告较完整，内容较丰富、图文并茂，文字足够且基本正确，对实验方案有自己的思路与见解。
	79.9 至70%	根据实验要求基本实现主要功能。实验态度较为认真，基本理解实验要求，解决问题能力一般，沟通协作能力一般。	实验报告较完整，内容较丰富，文字内容足够且基本正确。
	69.9% 至60%	根据实验要求实现主要功能但有一些遗漏。实验态度一般，基本理解实验要求，解决问题能力一般，沟通协作能力一般。	实验报告基本完整，内容基本够，有少量错误。
	59.9%至0	无法实现主要功能，同时完成附加任务要求。实验态度认真，充分理解实验要求，解决问题能力强，沟通协作很好。	实验报告未完成，内容不够，错误多。

五、参考学习资料

课程教材：人工智能数学基础，廖盛斌著，电子工业出版社，2023年9月，ISBN：9787121463075。

推荐教材1：人工智能数学基础，唐宇迪著，北京大学出版社，2020年10月，ISBN：9787301314319

推荐教材2：人工智能的数学基础，冯朝路著，清华大学出版社，2022年8月，ISBN：9787302603818

上一条返回列表

《人工智能的数学基础》《Mathematical Basis of Artificial Intelligence》教学大纲

友情链接：